Monty Hall, il quesito rivelatore

C’è un quesito matematico che diventa un tarlo per quanto l’assunto cui esso giunge è contro-intuitivo. La nostra mente si rifiuta di accettare quella che è a tutti gli effetti un’evidenza sia dal punto di vista della sua dimostrazione teorica che da quello sperimentale. La nostra mente si rifiuta, ma forse proprio in quell’illogicità risolta risiede un’illuminazione che trovo incredibilmente affascinante!

Monty Hall, così si chiama il quesito in questione, dal nome di un presentatore che conduceva un celebre gioco a premi alla tv canadese.
Ma veniamo al dunque.

In questo gioco a premi un oggetto di grande valore, diciamo un’automobile, è nascosto dietro una sola di tre porte chiuse. Dietro le altre due c’è una capra. Dopo aver scelto una porta, diciamo per semplicità la prima, il presentatore apre la numero 3, rivelando che il contenuto è quello di minor valore (beeehhhh…)
A questo punto il conduttore vi chiede: “confermate la scelta della porta numero 1 o volete cambiare?”
Qual è secondo voi la scelta più vantaggiosa?

Pensateci bene, anzi non pensateci affatto perché la vostra mente, nel ragionamento vi condurrà su una strada che è sicuramente sbagliata!
Chiunque infatti – compresi fior fior di matematici che si sono fermamente opposti a ciò cui inaspettatamente questo esperimento conduce – a questo punto è portato a pensare che le possibilità di vittoria da una su tre siano diventate una su due, rendendo assolutamente equivalenti la scelta di restare sulla prima porta e quella di cambiare idea passando alla seconda. Ebbene no!

Ma rivediamo meglio i passaggi del quesito quesito avvalendoci di deliziosi disegni esplicativi:

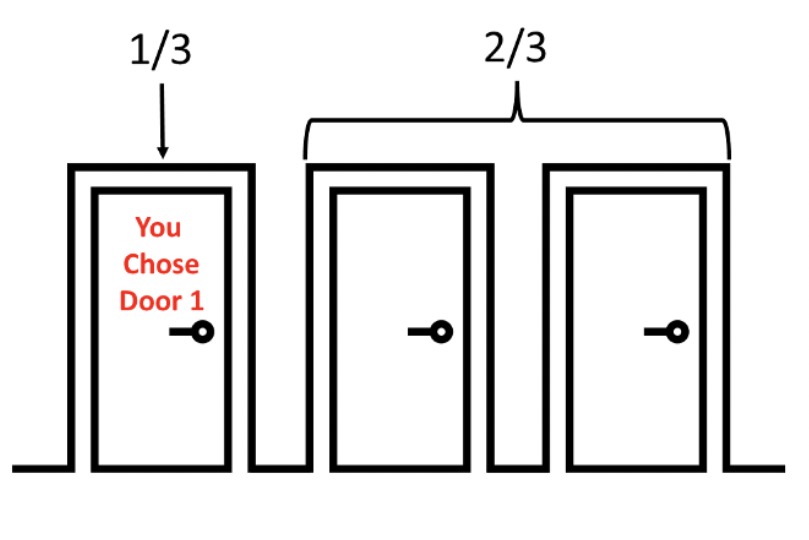
Abbiamo scelto la porta numero 1 e siamo tutti d’accordo nel ritenere che la nostra probabilità di vincere l’auto sia 1/3 (il 33,33%), mentre quella di perdere sia di 2/3. Che accade quando il presentatore apre una porta, diciamo la numero 3, rivelando la capra?
Ci verrebbe da dire che, scartata la terza porta, il gioco si riconduca ad una versione ridotta con solo due porte. Avremmo allora il 50% di probabilità di indovinare e cambiare o non cambiare la nostra scelta diventa un atto totalmente inutile ai fini statistici.
E invece no! Per strano che sembri, se restiamo fermi sulla nostra scelta iniziale continuiamo ad avere 1/3 di probabilità di indovinare, ma se scegliamo la seconda (l’unica per la quale ancora non si sappia il contenuto) ne abbiamo 2/3!
Magicamente il “terzo” di probabilità della porta aperta si è trasferito sulla seconda, raddoppiandone la probabilità : 1/3+1/3 = 2/3, ecco che cambiando la nostra scelta abbiamo ora il 66,66 % di probabilità di vincere.

La cosa resta vera anche se avessimo inizialmente scelto la porta 2 al posto della 1! In questo caso sarebbe stata la prima porta ad aumentare la sua probabilità di essere quella giusta.
La cosa resta vera anche se le porte diventano 4, 50, 100 o un milione! Una volta fatta, DA VOI, la scelta questa manterrà la percentuale di possibilità di vittoria che VOI le avete assegnato, mentre tutte quelle che si apriranno dopo rivelando fino alla penultima il loro contenuto di capre e caproni “spalmeranno” il loro potenziale di vittoria solo sull’altra porta, quella che VOI non avete scelto, l’unica che non avete in qualche modo designato con la VOSTRA decisione!

Ora lo so che state pensando che questa cosa non può essere, che non c’è nessuna logica e nessun motivo razionale per cui le cose vadano così ma credetemi anche i fior fiore di matematici di cui sopra alla fine hanno dovuto arrendersi all’evidenza, teorica e pratica di tale conclusione.
In calce all’articolo trovate il codice del programma in Phyton che simula questa situazione e che potrete eseguire tutte le volte che vorrete per scoprire che alla fine sarà SEMPRE più conveniente, dal punto di vista delle probabilità di vittoria, cambiare quella stramaledetta porta!

Quello che come accennavo all’inizio trovo estremamente affascinante in tutta la faccenda mi è apparso di colpo come un’evidenza proprio grazie ai deliziosi disegni esplicativi di cui sopra. Quella scritta in rosso “You chose” mi ha mostrato la potenza dell’atto volontario del designare, del decidere coscientemente di dirigere un’intenzione che resta tale. È una cosa potentissima che non solo conferisce alla nostra decisione la qualità dell’irreversibilità, ma la distingue dal magma dell’indefinito che ne resta al di fuori e che è la sola cosa che a quel punto può davvero cambiare.

Ecco il programma in Python:

import numpy as np
#import altair as alt
import pandas as pd
import time
#alt.renderers.enable(‘mimetype’)

nb_games = 10000000 # The number of games we’re going to simulate

print(“number of simulations:”,nb_games)  

Start_time = time.time()

games = []
for i in range(nb_games):
    game = np.repeat(‘

‘, 3)
    prize = np.random.randint(0,3,1) # the door behind which the car is hidden
    game[prize]=’

‘
    games.append(game)

    wins=0 # win counter
for i in range(nb_games):
    doors = [0,1,2]
    player_door_choice = int(np.random.choice(doors, 1)) # the player initial’s door choice
    doors.remove(player_door_choice) # doors not chosen by player
    for j in doors: # Monty Hall reveals that behind one of the door not chosen is a goat
        if games[i][j] == ‘

‘:
            goat_door = j
    if games[i][player_door_choice] == ‘

‘: # The player keeps his initial door choice
        wins += 1

print(f”Not changing: Winning percentage: {round(wins/nb_games*100,1)}%”)

wins=0
for i in range(nb_games):
    doors = [0,1,2]
    player_door_choice = int(np.random.choice(doors, 1)) # the player initial’s door choice
    doors.remove(player_door_choice) # doors not chosen
    for j in doors: # Monty Hall reveals that behind one of the door not chosen is a goat
        if games[i][j] == ‘

‘:
            goat_door = j
    doors.remove(goat_door) # the player changes its door choice
    if games[i][doors[0]] == ‘

‘:
        wins += 1

print(f”Switching door: winning percentage: {round(wins/nb_games*100,1)}%”)
print(f’\nSimulation Completed in: {round(time.time()-Start_time,2)} Seconds’)